Centroid of a triangle properties

The centroid of the triangle is the point at which the three medians intersect that is the centroid is the point of intersection between the three lines each of which pass through a vertex of the triangle and the midpoint of the opposite leg as shown in the diagram below. It is the point where all the medians meet.

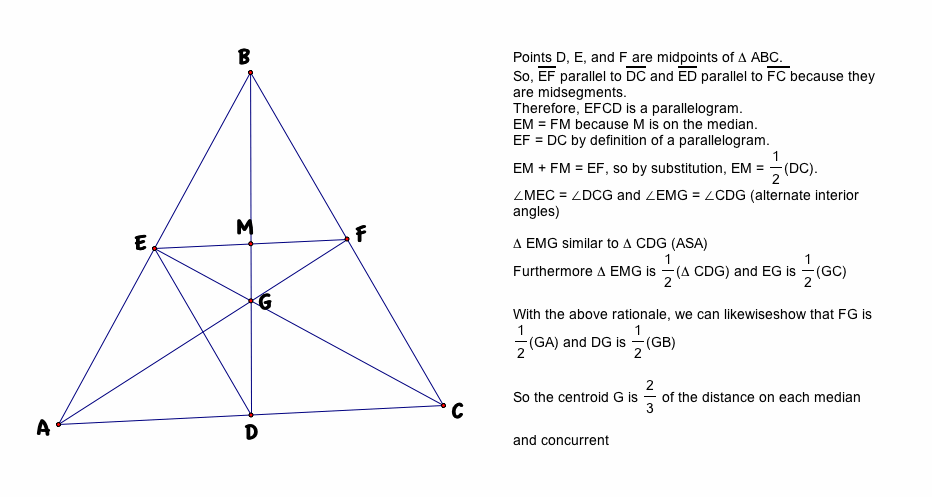
Segments AD where D bisects BC BE with E bisecting AC and CF F bisecting AB.

Centroid of a triangle properties. The centroid is an important property of a triangle. Let us discuss the definition of centroid formula properties and centroid for different geometric shapes in detail. The centroid is the centre point of the object.

The point in which the three medians of the triangle intersect is known as the centroid of a triangle. It is also defined as the point of intersection of all the three medians. The Centroid is a point of concurrency of the triangle.

It is the point where all 3 medians intersect and is often described as the triangles center of gravity or as the barycent. Properties of the Centroid. It is formed by the intersection of the medians.

It is one of the points of concurrency of a triangle. The centroid of a triangle is the intersection of the three medians or the average of the three vertices. It has several important properties and relations with other parts of the triangle including its circumcenter orthocenter incenter area and more.

The centroid is typically represented by the letter. Mathematically a centroid of a triangle is defined as the point where three medians of a triangle meet. It is one of the three points of concurrency in a triangle along with the incenter circumcenter and orthocenter.

A centroid is represented typically by the symbol G. The centre point of the object is what we refer to as the centroid. The point at which a triangles three medians intersect is called the centroid of the triangle.

We can also define the centroid as the point of intersection of the three medians. The median refers to the line joining the midpoint of a side to the opposite vertex of a triangle. The triangles centroid divides the median in the ratio 21.

The centroid is the point where the three medians of the triangle intersect. It has the following properties. The centroid is always located in the interior of the triangle.

The centroid is located 23 of the distance from the vertex along the segment that connects the vertex to the midpoint of the opposite side. Click to see full answer. The centroid of the triangle is the point at which the three medians intersect that is the centroid is the point of intersection between the three lines each of which pass through a vertex of the triangle and the midpoint of the opposite leg as shown in the diagram below.

It is relatively easy to find the centroid of a triangle that sits in the coordinate plane. Let a triangle in the plane. It is located inside the object.

It is the center point of the object. It is the point where all the medians meet. Consider a triangle ABC whose vertices are Ax 1 y 1 Bx 2 y 2 Cx 3 y 3 Thus the centroid is calculated by taking the average of all the three vertices by using the formula as mentioned below.

Centroid of a triangle x 1. In this video we will know median and centroid of a triangle and its some properties. Centroid G is also known as the Center of Gravity of a triangle.

The Center of Gravity CG is merely the balancing point of an object. For instance the CG. Of a 10 inch stick is 5 inches.

If the stick is made of the same material and has the same weight inch-for-inch it will balance when supported or pivoted at its 5 inch mark. Home Documents Properties of triangles - Centroid Properties of triangles - Centroid. 6 Properties of triangles - Centroid Properties of triangles - Centroid.

6 Date post. The centroid of a triangle is that balancing point created by the intersection of the three medians. If the triangle were cut out of some uniformly dense material such as sturdy cardboard sheet metal or plywood the centroid would be the spot where the triangle would balance on the tip of your finger.

Median of a Triangle. On Centroids of Triangles David Hornbeck September 27 2013 In this write-up we will discuss centroids of triangles - what they are where they are and how to prove some features of them. The centroid of a triangle 4ABC is the intersection of all three medians of a triangle ie.

Segments AD where D bisects BC BE with E bisecting AC and CF F bisecting AB. It is convention to label this. Properties of a triangle.

These are the properties of a triangle. A triangle has three sides three angles and three vertices. The sum of all internal angles of a triangle is always equal to 180.

This is called the angle sum property of a triangle. The sum of the length of any two sides of a triangle is greater than the length of the third. This is the point of intersection of the medians of the triangle and is conventionally denoted mnemonic.

The centroid has the special property that for each median the distance from a vertex to the centroid is twice that of the distance from the centroid to the midpoint of the side opposite that vertex.