Perpendicular bisector of a chord

Conversely the line segment through O bisecting SR is perpendicular to SR. The length of a chord increases as the perpendicular distance from the center of.

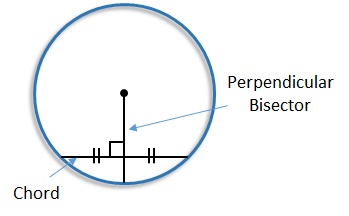
Properties of a Chord The radius of a circle is the perpendicular bisector of a chord.

Perpendicular bisector of a chord. The perpendicular line from the center of a circle O bisects the chord SR. Conversely the line segment through O bisecting SR is perpendicular to SR. Drag the brown point A to change the figure.

Conversely the line segment through O bisecting SR is perpendicular to SR. More About the Circle Theorem where the Perpendicular Bisector of a Chord Passes Through the Center of a Circle A line that is perpendicular to a chord and bisects it must pass through the center of the circle. A line that is perpendicular to a chord and.

Here we can apply the chord bisector theorem which states that if we have a circle with center 𝑀 containing a chord 𝐴 𝐵 then the straight line that passes through 𝑀 and bisects chord 𝐴 𝐵 is perpendicular to 𝐴 𝐵. Hence we can say that 𝑚 𝑀 𝐶 𝐵 9 0. Circle Theorem Proof - The perpendicular bisector of any chord of a circle passes through the centre of the circle.

Proof that the line drawn from the centre of a circle perpendicular to a chord bisects the chord. Perpendicular Bisector of a Chord. Perpendicular Bisector of a Chord Conjecture.

The cordof a circle is a segment whose endpoints are on the circle. This conjecture states that the perpendicular bisector of any chord passes through the center of the circle. Understand that the straight line passing through the center of the circle which is also perpendicular to a chord bisects this chord and solve problems to find unknown lengths understand that the perpendicular bisector of any chord in a circle passes through the center of this circle.

In this example we teach you the method of constructing perpendicular bisectors of two chords and finding their meeting pointVideos in the playlists are a. Basic properties of Chords in a circle. Also an introduction to perpendicular bisector.

Check out wwwmathwithmrbarnesca for more math videos and practice p. The perpendicular bisector of a chord is the line that cuts the chord in half at a right angle. The perpendicular bisector of a chord passes through the centre of the circle.

This theorem is covered in this video on circle theorems. The chord bisector theorem can be summarized in three ways. Firstly if we have a circle with center 𝐴 containing a chord 𝐵𝐶 then the straight line that passes through 𝐴 and bisects the chord 𝐵𝐶 is perpendicular to 𝐵𝐶.

In the same way the straight line that passes through 𝐴 and is perpendicular to 𝐵𝐶 also bisects 𝐵𝐶. The converse of these two states that the perpendicular bisector of the chord 𝐵𝐶 passes. The perpendicular bisector of a segment A B is the locus of points M equidistant from A and B.

This means M A M B. But if we set M A R then this means A B are on the circle of centre M and radius R. And since the chord in this case is precisely A B and M.

Perpendicular bisector In the diagram below AB is the chord of a circle with centre O. OM is perpendicular to AB meet at a right angle. Look at triangles OAM and OBM.

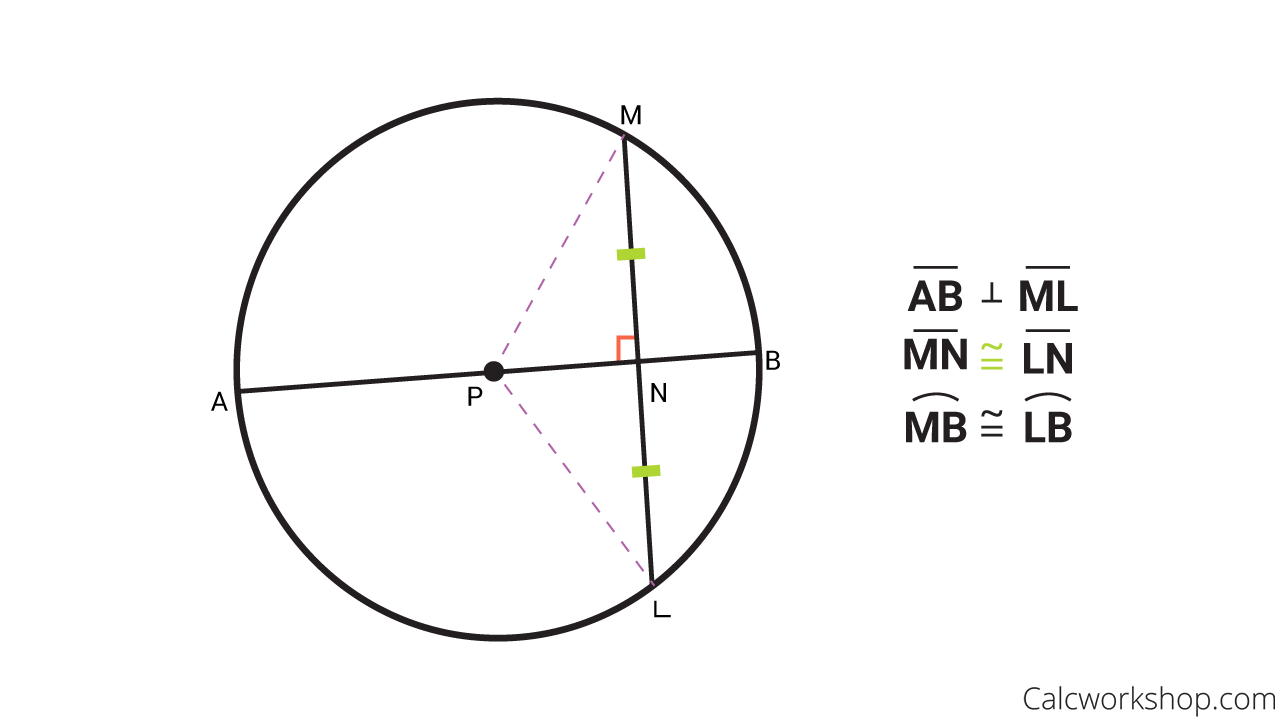
Perpendicular Chord Bisector Converse If one chord of a circle is a perpendicular bisector of another chord then the first chord is a diameter. Statements Reasons is the perpendicular bisector of in the circle Given Plot L the center of the circle. Draw 𝐿 and 𝐿 Through any two points there is.

In the above circle if the radius OB is perpendicular to the chord PQ then PA AQ. The perpendicular bisector of a chord passes through the center of a circle. In the above circle OA is the perpendicular bisector of the chord PQ and it passes through the center of the circle.

A Radius That Is Perpendicular To A Chord Acts As The Perpendicular Bisector Of That Chord. CE-256 G BE 250 14-12–0-0- Part D Write A Paragraph Proof Of Your Conclusion In Part C. To Begin Your Proof Draw Radii OAand OC.

B IV X X Font Sizes A- Prove. A Radius That Is Perpendicular To A Chord Acts As The Perpendicular Bisector Of That Chord. The perpendicular bisector of a chord.

Contains the circles center. Divides the chord into two congruent segments bisects the chord is perpendicular to the chord. Properties of a Chord The radius of a circle is the perpendicular bisector of a chord.

The length of a chord increases as the perpendicular distance from the center of.